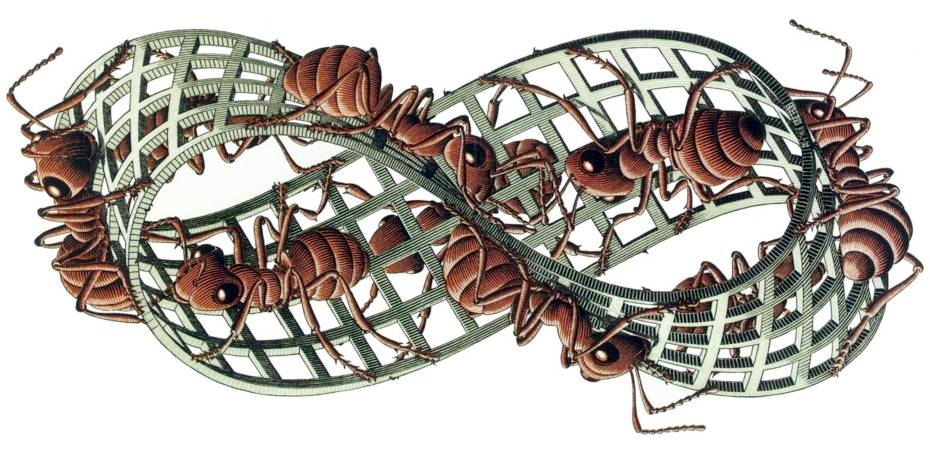
il Nastro di Moebius

Le superfici ordinarie, quelle degli oggetti comuni, hanno sempre due facce e questo vale sia per le superfici chiuse (prive di contorno, come la sfera) che per quelle aperte (delimitate da un perimetro, come un rettangolo). Una formica che si trovi su una faccia del rettangolo non potrà mai raggiungere del cibo sull'altra faccia, se c’è dell'insetticida lungo tutto il bordo. Similmente se consideriamo una mosca fuori da una sfera di cristallo e del cibo posto all'interno, la mosca non riuscirà mai a raggiungere il cibo.
Tuttavia esistono oggetti per cui tale principio viene a mancare ed il più noto di questi è senza dubbio è il cosiddetto Nastro di Moebius in cui le due facce sono coincidenti e quindi ha una sola faccia ed un solo bordo. La sua superficie risulta essere infinitamente percorribile: la formica può raggiungere il cibo in qualunque posto del nastro si trovi.
Il nastro deve il suo nome al matematico August Ferdinand Moebius (1790-1860) che fu il primo a studiare le sue caratteristiche, topologicamente molto interessanti.
Un nastro di Moebius può essere facilmente realizzato partendo da una striscia rettangolare ed unendone i lati corti dopo aver impresso ad uno di essi mezzo giro di torsione. Se si percorre il nastro con una matita, partendo da un punto casuale, si noterà che la traccia si snoda sull'intera superficie del nastro che è quindi unica.